Sai Sampath Kedari
Robotics & AI — Inference, Learning, and Control Under Uncertainty
Bayesian modeling, estimation, and decision-making in real-world robotic systems
I work in Robotics & AI on the part of the problem that decides what a robot should do next when it does not fully know what is happening. Real robots operate with noisy sensors, incomplete information, and changing environments. What interests me is how a robot can form an internal understanding of the world, keep updating it with experience, and use it to choose actions over time.
At a high level, I build systems that combine “what’s going on” with “what should I do next.” This means representing uncertainty explicitly, updating beliefs as new data arrives, and using those beliefs to guide decisions rather than relying on fixed rules or perfect information. I am especially drawn to problems where learning and decision-making happen together, instead of being treated as separate steps.
So far, my work has focused on probabilistic inference methods such as Monte Carlo techniques and Bayesian filtering to model uncertainty over hidden states and unknown quantities. I am now extending this toward sequential decision-making and robot learning, studying probabilistic graphical models, MDPs and POMDPs, and reinforcement learning. My goal is to build robotic systems that improve their behavior through experience by continually refining their internal beliefs and using them to make better decisions.
- Probabilistic state-space modeling and Bayesian inference for robotic systems, with an emphasis on joint estimation of hidden states and unknown parameters under uncertainty using Monte Carlo methods and Bayesian filtering and smoothing.
- Probabilistic graphical models for sequential systems, including Bayesian Networks and Dynamic Bayesian Networks, focusing on exact and approximate inference, belief propagation over time, and learning structured representations from data.
- Sequential decision-making under uncertainty, studied through dynamic programming, Markov Decision Processes, and Partially Observable Markov Decision Processes, where actions are chosen based on evolving belief states rather than full observability.
- Robot learning as belief-driven decision-making, exploring reinforcement learning and deep reinforcement learning as endpoints for policies that act on uncertain, learned internal representations instead of fixed models.
-
University of Michigan, Ann Arbor
M.S. Mechanical Engineering (Robotics), Jan 2023 – Apr 2024 - University of Michigan, Ann Arbor
M.S. Automotive Engineering, Aug 2021 – Dec 2022 -
National Institute of Technology, Rourkela, India
B.Tech. Mechanical Engineering, Jul 2015 – May 2019
Monte Carlo Statistical Methods
State estimation, parameter learning, sensor fusion, policy evaluation, and uncertainty-aware planning — across the robot learning stack, many core problems reduce to computing expectations over complex, high-dimensional, nonlinear distributions. Exact analytical solutions are intractable.
Monte Carlo methods address this by replacing integration with sampling, approximating distributions with empirical ones and enabling expectation estimates when closed-form inference is not possible.
This project is a full mathematical reconstruction of Robert & Casella's Monte Carlo Statistical Methods, including importance sampling, MCMC, control variates, variance reduction, and more. Every algorithm is implemented from first principles, with a focus on statistical rigor, numerical reliability, and deep understanding of probabilistic inference.
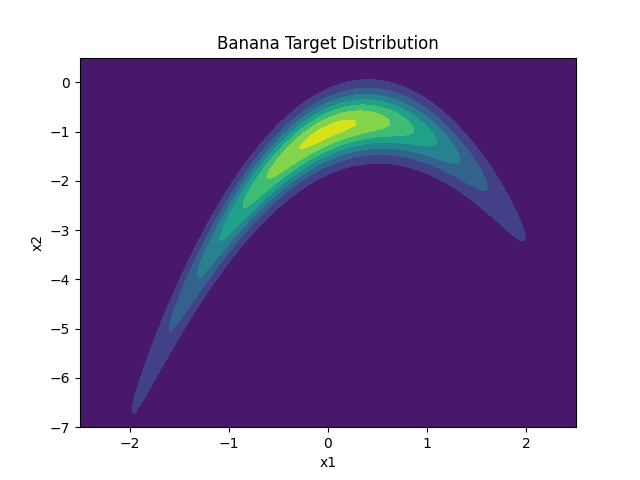
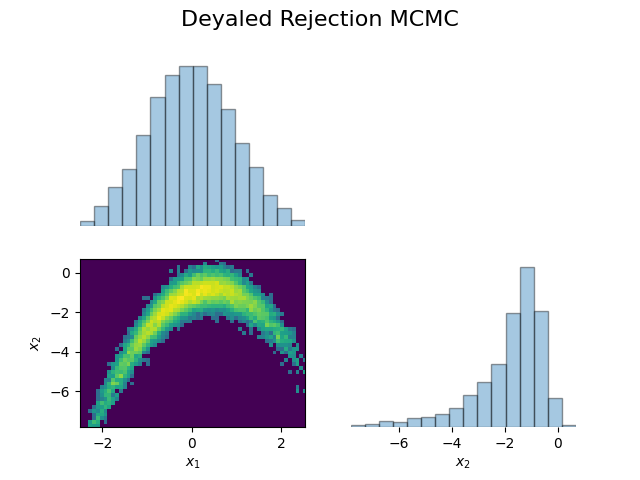
DRAM: Delayed Rejection Adaptive Metropolis on a Banana Distribution
A two-stage DRAM sampler combining delayed rejection with adaptive covariance updates to efficiently explore the curved banana distribution, showing how refined secondary proposals and empirical covariance learning improve acceptance and mixing on difficult target geometries.
Inverse Transform Sampling for Beta Distribution
Uniform samples \( U \sim \mathrm{Unif}(0,1) \) are passed through the inverse Beta CDF \( F^{-1}(U) \) to produce exact \( \mathrm{Beta}(10,3) \) draws. This demonstrates the core idea of inverse transform sampling: shaping uniform randomness into a target distribution and visualizing the empirical convergence to its true density.
Accept–Reject Sampling: Gaussian Target with Laplace Proposal
Samples are drawn from a Laplace proposal and accepted with probability \( \frac{f(x)}{M g(x)} \), where \( M g(x) \) envelopes the Gaussian target. The plot highlights how the shape differences between the Gaussian and Laplace distributions determine acceptance rates and sampling efficiency.
Bayesian Filtering & Smoothing
Robotic systems must operate with noisy sensors, partial observability, uncertain dynamics, and unmodeled disturbances. In problems such as localization, state estimation, sensor fusion, contact estimation, and disturbance rejection, the true system state is never directly observed and errors compound over time. Reliable operation therefore requires tracking belief over the robot's state, not just a single best estimate.
Bayesian filtering and smoothing address this by formulating state estimation as recursive probabilistic inference in dynamical systems. Instead of estimating states independently at each time step, these methods propagate uncertainty through system dynamics and update beliefs using incoming measurements, explicitly accounting for sensor noise, modeling error, and partial observability.
This repository implements Bayesian filtering and smoothing methods used across robotics, including Kalman and Gaussian filters for linear and locally linear systems, and sampling-based filters built on Sequential Importance Sampling with resampling for nonlinear, non-Gaussian settings. Applications include localization, sensor fusion, contact and force estimation, parameter learning, and uncertainty-aware control, with emphasis on how uncertainty is propagated and updated over time.
From a mathematical perspective, the project follows Särkkä's Bayesian Filtering and Smoothing, deriving the filtering and smoothing equations from the underlying joint distributions and implementing them from scratch. The focus is on statistical correctness, approximation assumptions, weight degeneracy, and understanding the limits of Gaussian and sampling-based estimators.
Batch vs Recursive Bayesian Linear Regression
Sequential Bayesian updates converge to the batch posterior, showing uncertainty contraction as data accumulates.
Extended Kalman Filter for State Estimation of a Nonlinear Pendulum
Local Gaussian filtering via linearization tracks nonlinear dynamics while exposing approximation error and covariance evolution.
Bootstrap Particle Filter (Sequential Importance Sampling with Resampling)
Non-Gaussian belief propagation using particles highlights weight degeneracy and the role of resampling under nonlinear dynamics.
Bayesian Inference
This repository studies Bayesian parameter estimation for nonlinear dynamical systems where posterior distributions are analytically intractable. Markov Chain Monte Carlo methods are used to approximate posterior expectations, enabling posterior mean estimation and uncertainty-aware predictive dynamics.
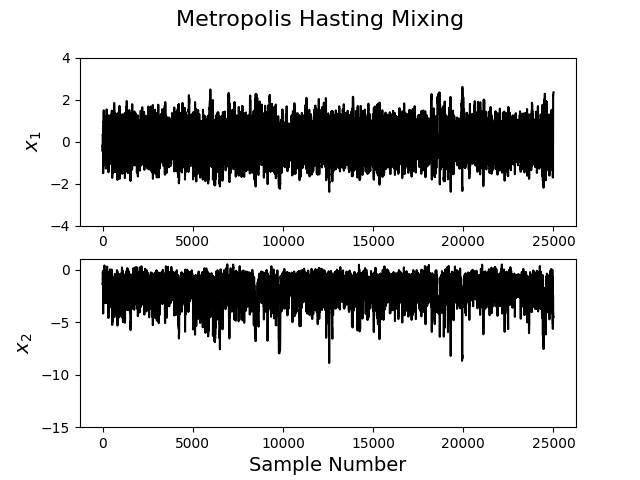
MCMC-Based Bayesian Inference for Nonlinear Dynamical Models
MCMC-based parameter estimation and posterior predictive analysis under nonlinear, non-Gaussian models.
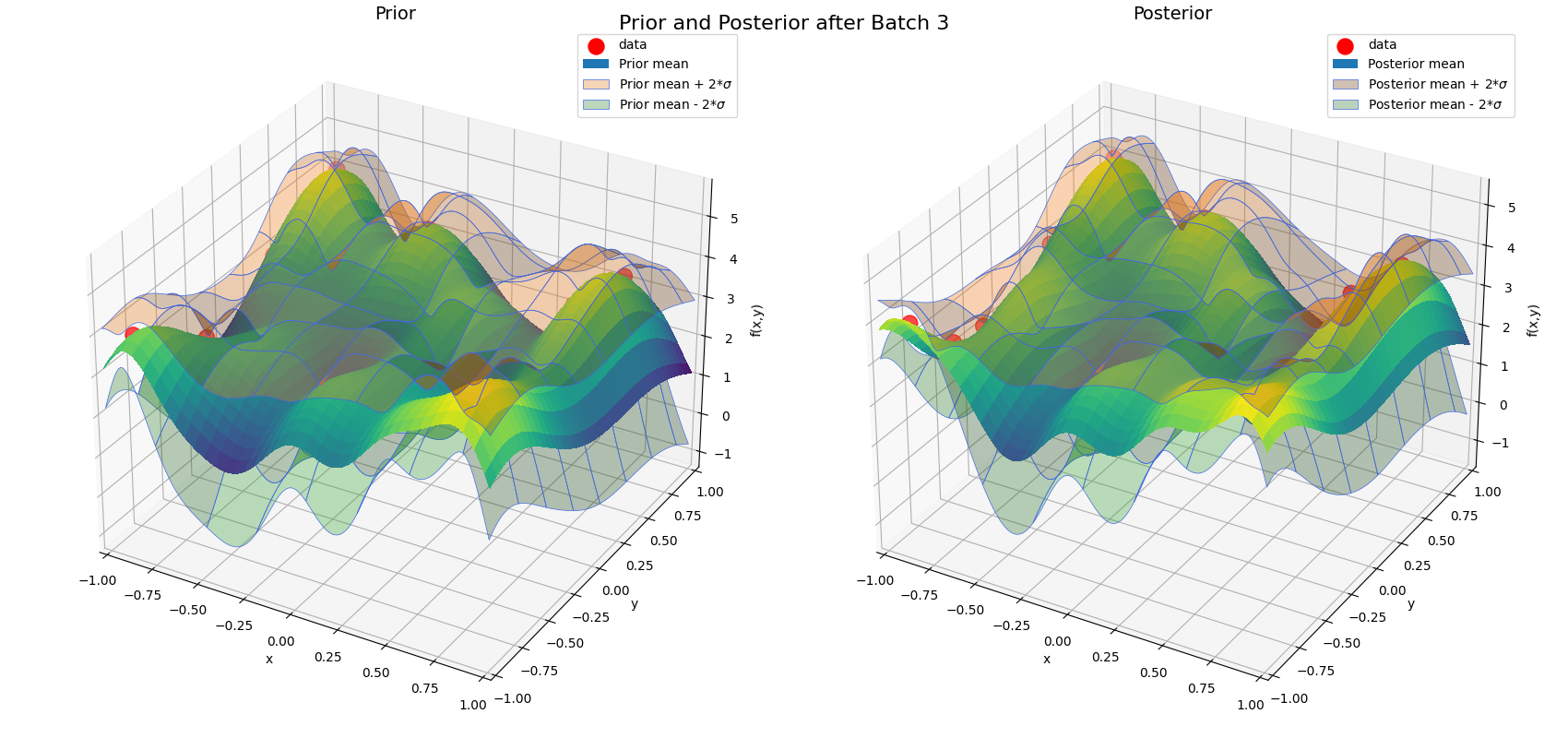
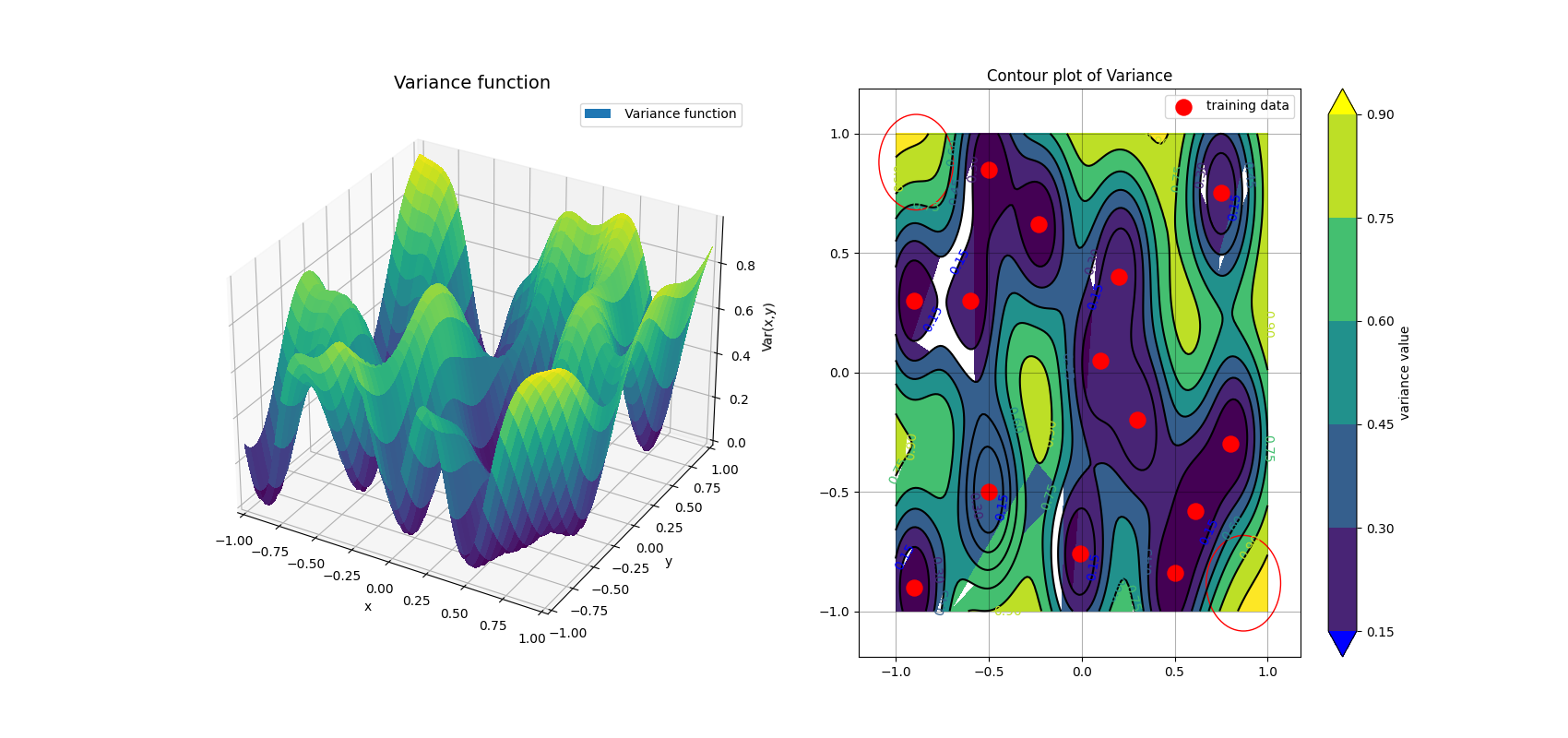
Active Object Localization using Bayesian Optimization
In this exploration-focused project, a robot models its environment with Gaussian Process regression and selects informative measurements via Bayesian Optimization. Expected Improvement and Probability of Improvement guide the search for a hidden target, demonstrating how uncertainty-aware policies accelerate localization.
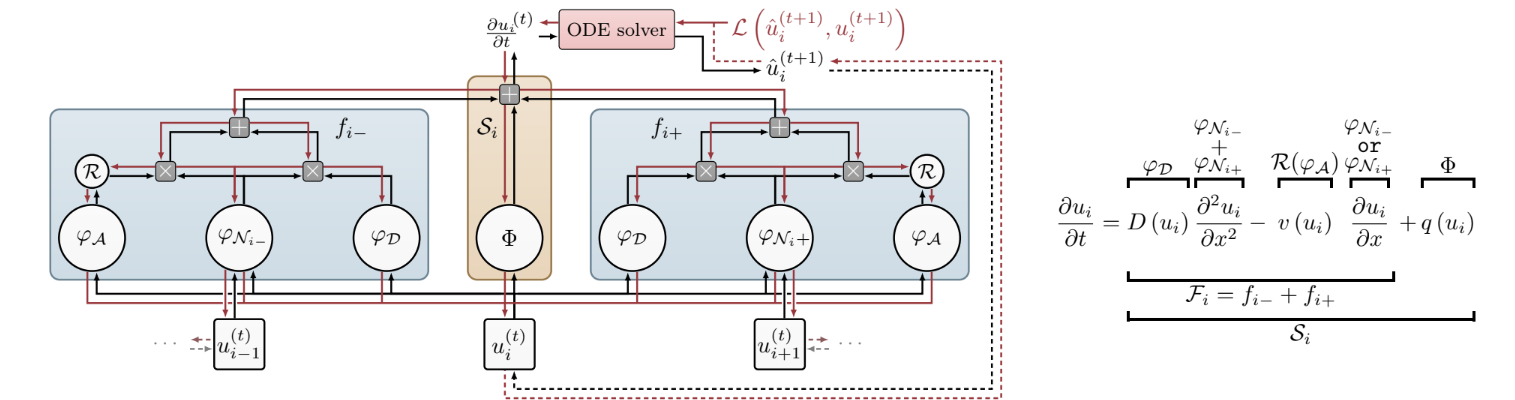
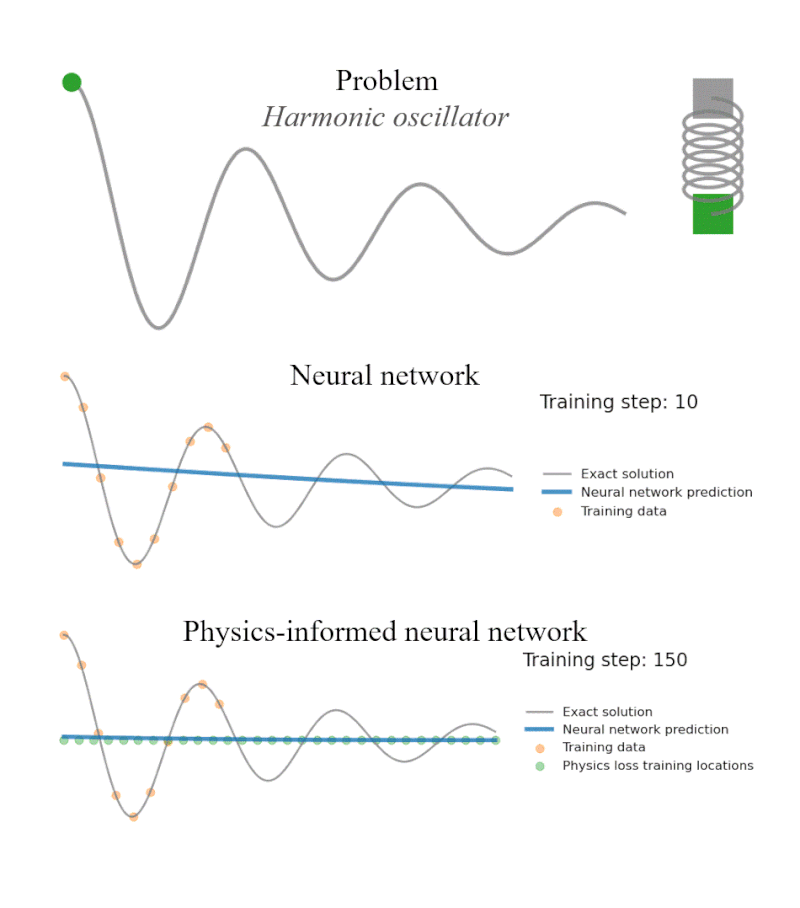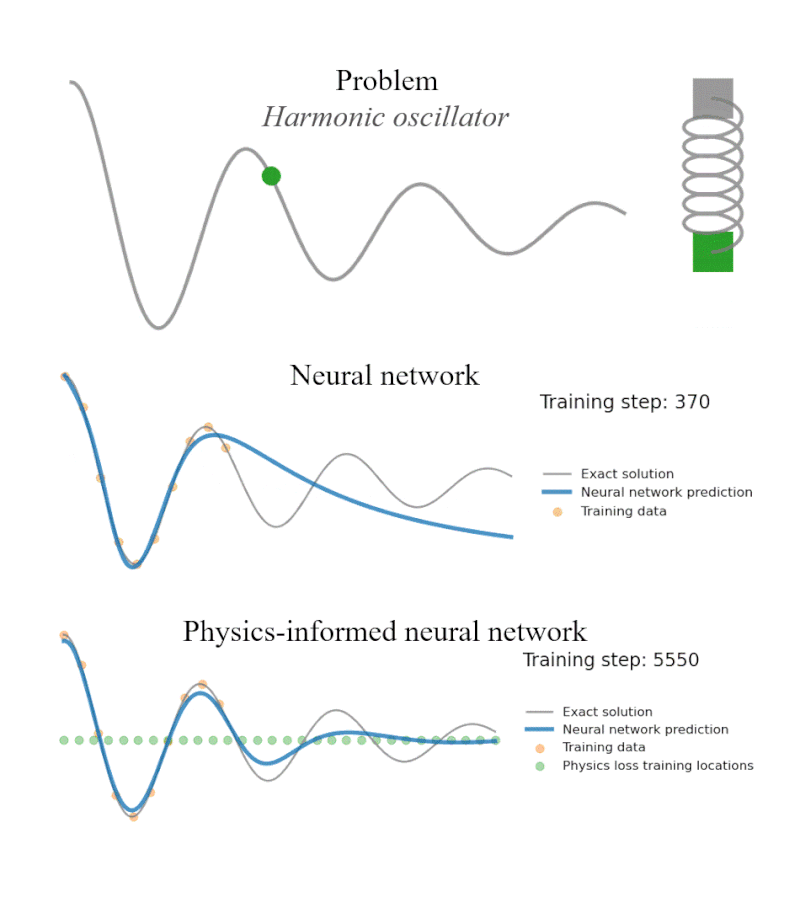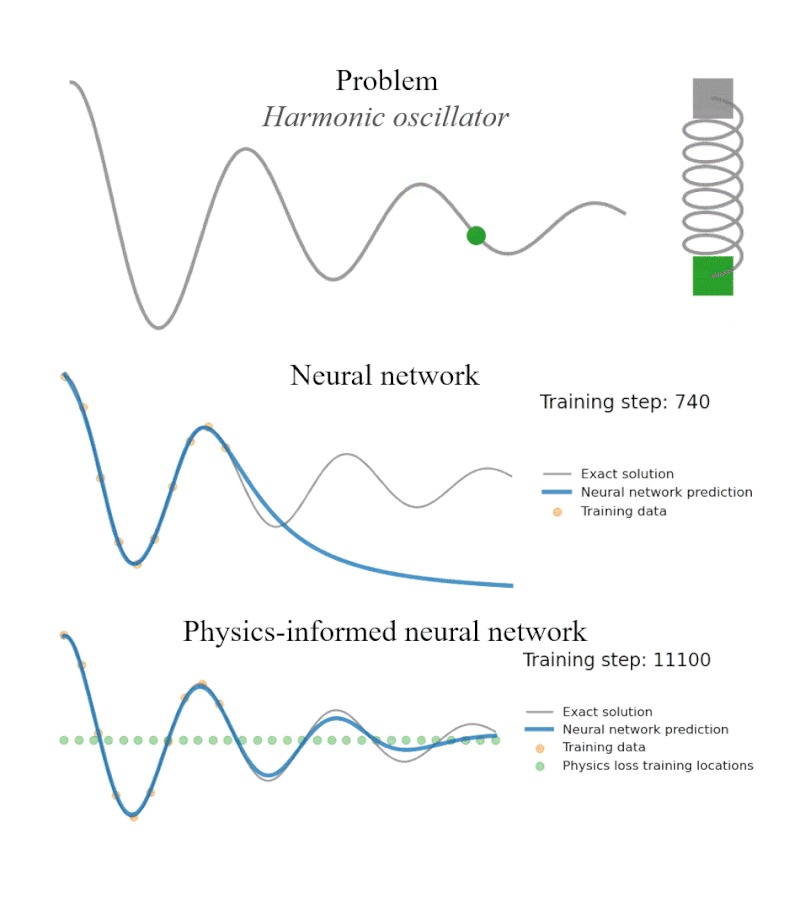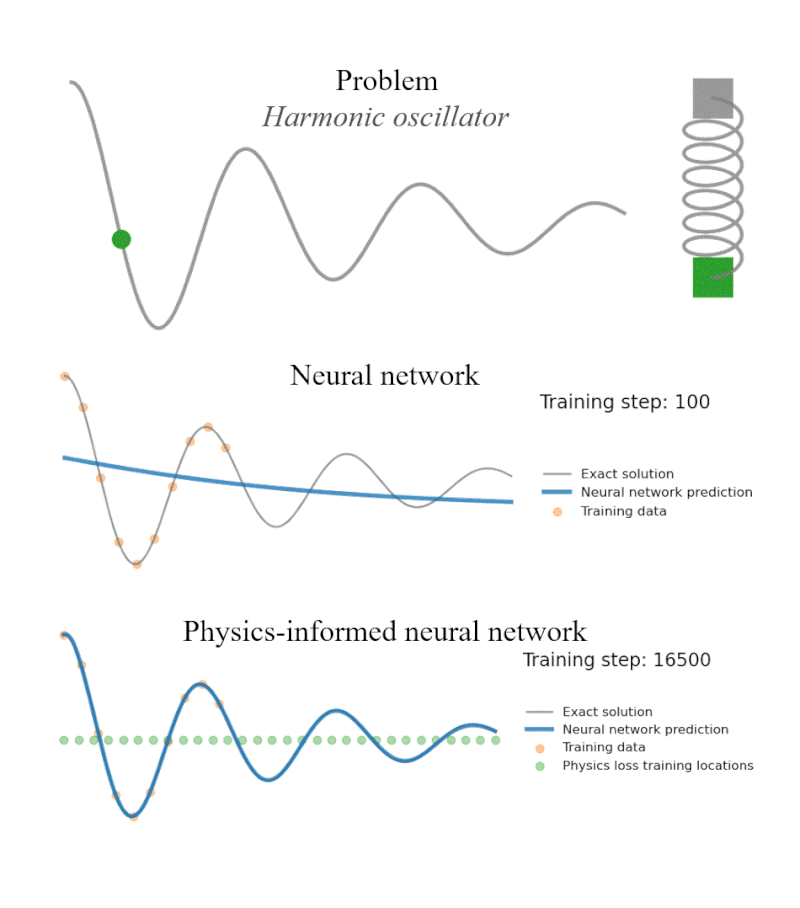
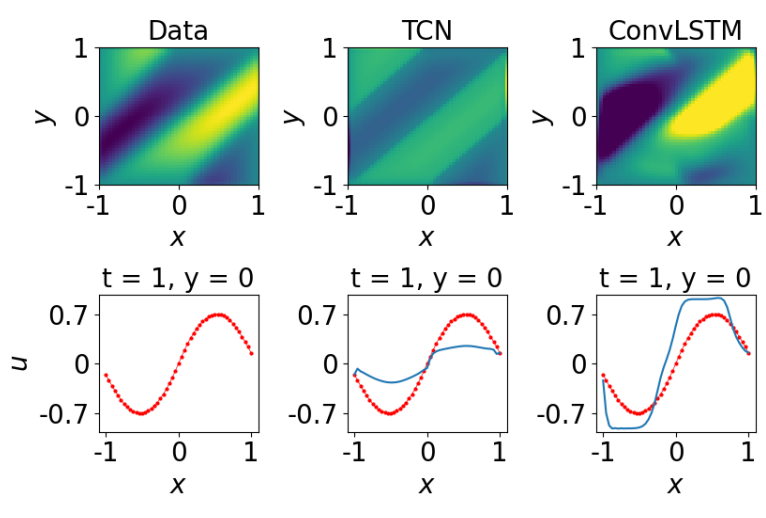
Reproducibility Study of Physics-Aware Neural Networks for PDEs
We replicated the FINN architecture to solve spatiotemporal partial differential equations, confirming its strong generalization and robustness. Experiments on Burgers', Allen–Cahn and diffusion-sorption systems showed FINN outperforming ConvLSTM, TCN and other baselines even with noisy data and longer prediction horizons.
Mathematics is the language of systems, uncertainty, and learning, essential for building intelligent and reliable robots. The work below reflects my commitment to mastering this foundation through deep study and rigorous problem-solving. Each GitHub repository represents a subject I have explored thoroughly, documenting both theory and exercises to build lasting intuition.
Statistical Inference Theory
Casella & Berger — Estimation, MLE, Bayesian inference, hypothesis testing. These exercises train the statistical thinking required for perception algorithms.
Probability and Distribution Theory
Casella & Berger — Random variables, expectation, exponential family, convergence theorems. Working through every problem strengthens my intuition for handling uncertainty in robotics.
Real Analysis
Kenneth Ross — Sequences, limits, continuity, uniform convergence, compactness. Building rigor here lets me prove convergence and stability of algorithms.
Convex Optimization
Stephen Boyd — Convex sets, functions, duality, gradient and interior-point methods. Solving problems equips me with tools for efficient planning and control.
Fourier Transform
Stanford EE261 — Fourier series, spectral representation, convolution, filters. A deep grasp of transforms aids processing sensor data and images.
Signals and Systems
Oppenheim — LTI systems, Laplace/Z/Fourier transforms, convolution, system stability. Understanding signals lays the groundwork for reliable dynamic models.
Differential Equations
MIT 18.03 & Edwards-Penney — Lecture notes and solved problems on first- and second-order ODEs, Laplace transforms, linear systems, and nonlinear dynamics. Essential for modeling real-world robotics and control systems.
Focus Areas: Machine Learning · Bayesian Inference · Convex Optimization · Control Theory · Statistical Estimation · Stochastic Processes · Nonlinear Dynamics
Dassault Systèmes
CATIA R&D Software Developer – Functional Tolerancing & Annotation (FTA)
Sep 2020 – Aug 2021 · Pune, India
- Contributed to the development of the Functional Tolerancing and Annotation (FTA) workbench in CATIA, a key module for managing 3D manufacturing data.
- Implemented optimizations for numerical methods and geometric computations to enhance the speed and robustness of the FTA module.
- Worked extensively on build systems and development tooling for large-scale C++ codebases, streamlining continuous integration and delivery pipelines.
Altair Engineering
HyperMesh & MotionView Software Developer
Sep 2019 – Sep 2020 · Bangalore, India
- Designed multibody dynamic (MBD) models of two- and four-wheelers using various suspension and powertrain architectures for the MotionView library; developed tire force visualization and a dynamic bicycle model for stability analysis.
- Improved solver performance in MotionView by optimizing core numerical methods and integrating C++ APIs with TCL/TK scripting for user customization.
- Contributed to HyperMesh development by creating and extending Commands (APIs) for pre-processing workflows and enabling deeper interaction between C++ and TCL/TK.
- PHYSICS 241 – General Physics II – Electricity & Magnetism
Fall 2022, Winter 2023 · University of Michigan, Ann Arbor - PHYSICS/BIOPHYS 151 – Introductory Physics Lab for Life Sciences
Spring 2023 · University of Michigan, Ann Arbor - PHYSICS 360 – Honors Physics III – Thermodynamics, Waves, and Relativity
Fall 2023, Winter 2024 · University of Michigan, Ann Arbor