Mathematical Foundations
Mathematics is the language of systems, uncertainty, and learning, essential for building intelligent and reliable robots. The work below reflects my commitment to mastering this foundation through deep study and rigorous problem-solving. Each GitHub repository represents a subject I have explored thoroughly, documenting both theory and exercises to build lasting intuition.
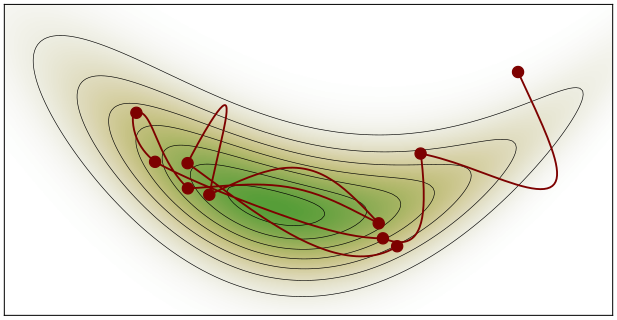
Monte Carlo Statistical Methods
A research-grade reconstruction of Monte Carlo Statistical Methods (Robert and Casella), built to expose the statistical engine behind modern AI, robot learning, and reinforcement learning. The project derives and implements the full Monte Carlo toolkit from first principles, including sampling, importance sampling, variance reduction, Brownian motion, and MCMC methods.
The work demonstrates how expectations are estimated in high dimensions, how posteriors behave under misspecification, how Monte Carlo estimators succeed or fail, and how MCMC explores complex distributions. These methods form the computational backbone of Bayesian inference, probabilistic state estimation, uncertainty propagation, and reinforcement learning in robotics.

Statistical Inference Theory
Casella & Berger — Estimation, MLE, Bayesian inference, hypothesis testing. These exercises train the statistical thinking required for perception algorithms.
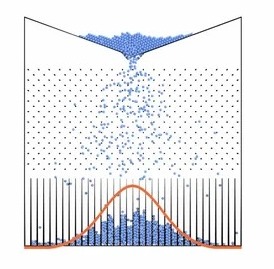
Probability and Distribution Theory
Casella & Berger — Random variables, expectation, exponential family, convergence theorems. Working through every problem strengthens my intuition for handling uncertainty in robotics.
Real Analysis
Kenneth Ross — Sequences, limits, continuity, uniform convergence, compactness. Building rigor here lets me prove convergence and stability of algorithms.

Convex Optimization
Stephen Boyd — Convex sets, functions, duality, gradient and interior-point methods. Solving problems equips me with tools for efficient planning and control.
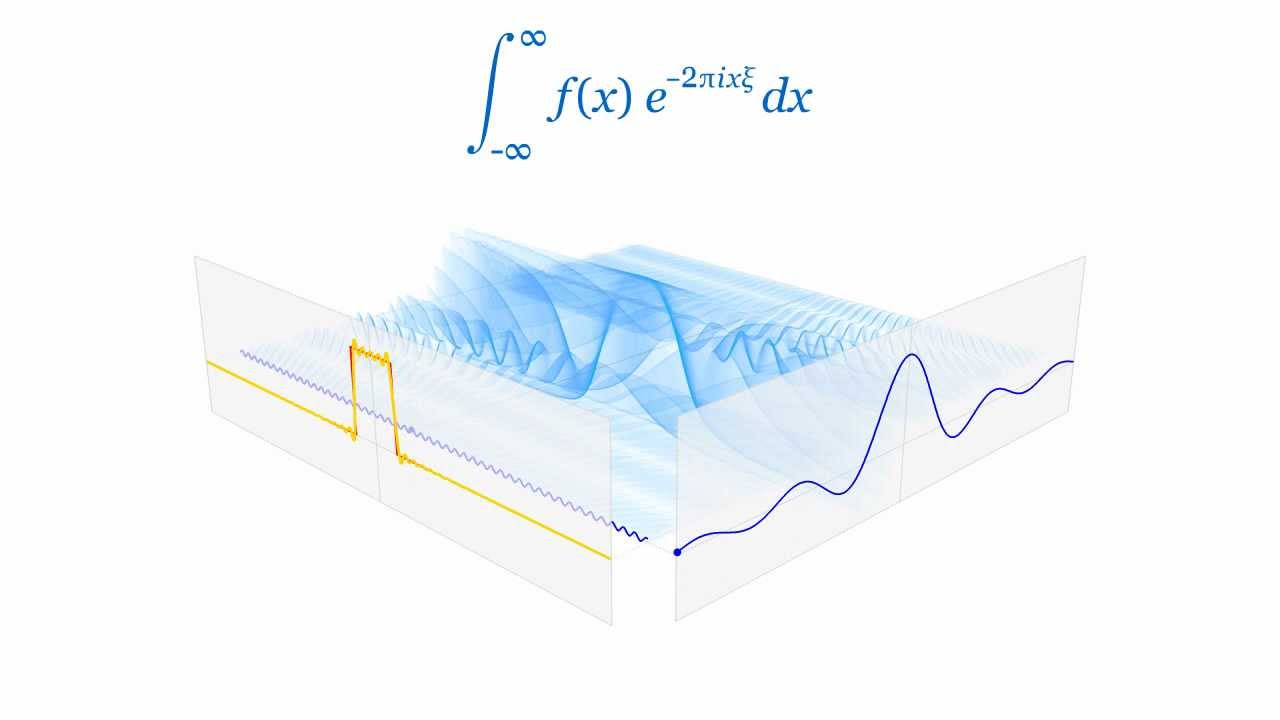
Fourier Transform
Stanford EE261 — Fourier series, spectral representation, convolution, filters. A deep grasp of transforms aids processing sensor data and images.

Signals and Systems
Oppenheim — LTI systems, Laplace/Z/Fourier transforms, convolution, system stability. Understanding signals lays the groundwork for reliable dynamic models.
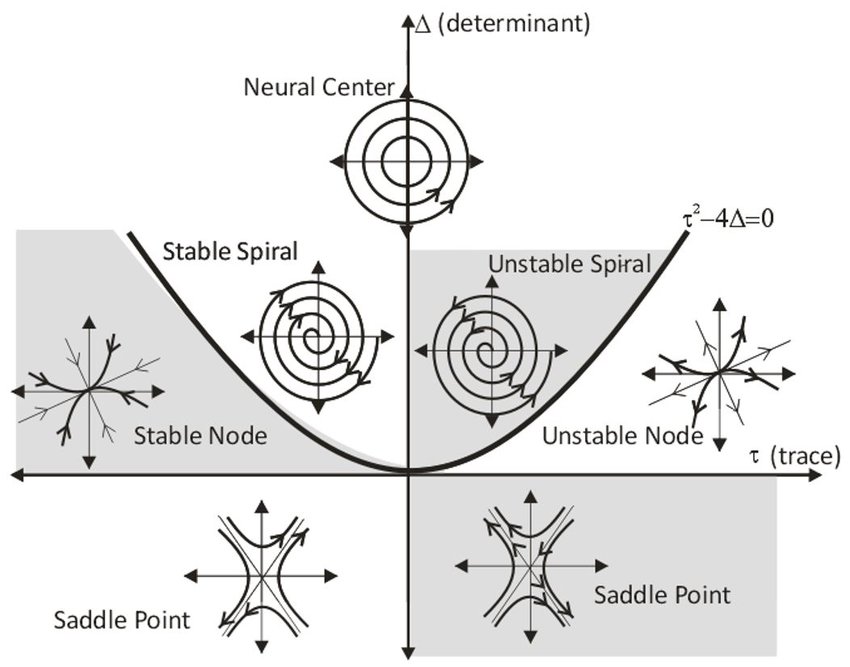
Differential Equations
MIT 18.03 & Edwards-Penney — Lecture notes and solved problems on first- and second-order ODEs, Laplace transforms, linear systems, and nonlinear dynamics. Essential for modeling real-world robotics and control systems.