Featured Projects
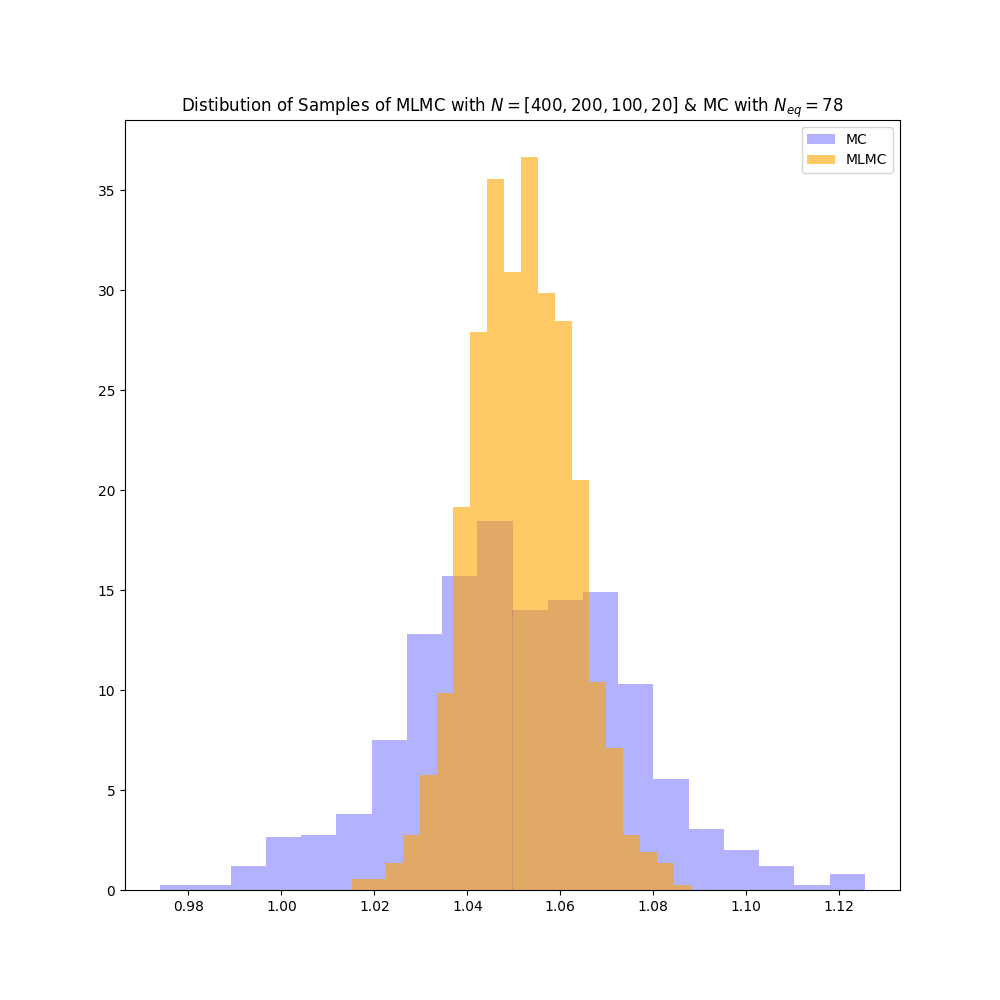
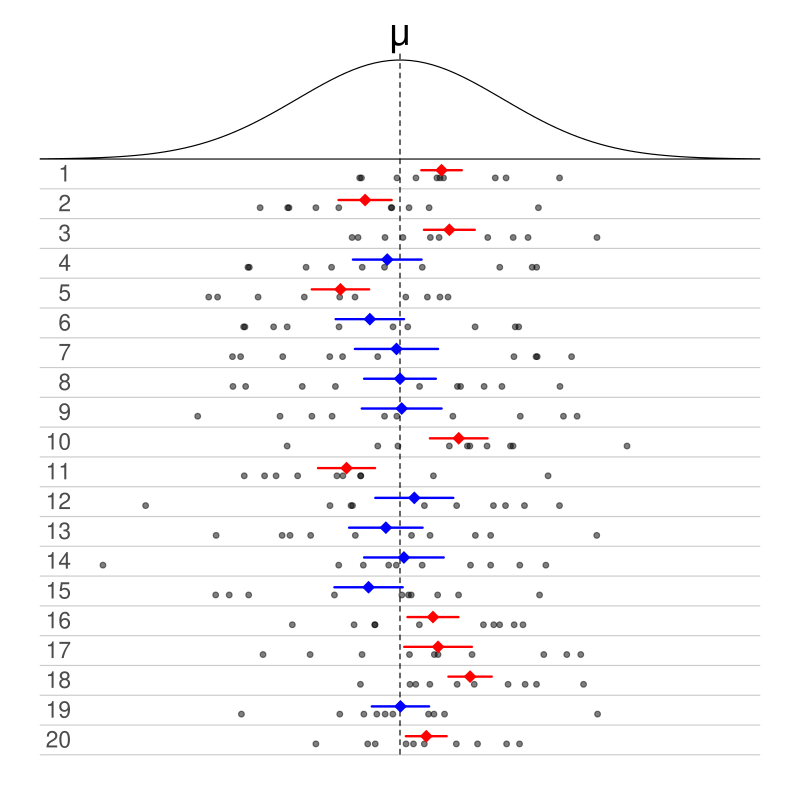
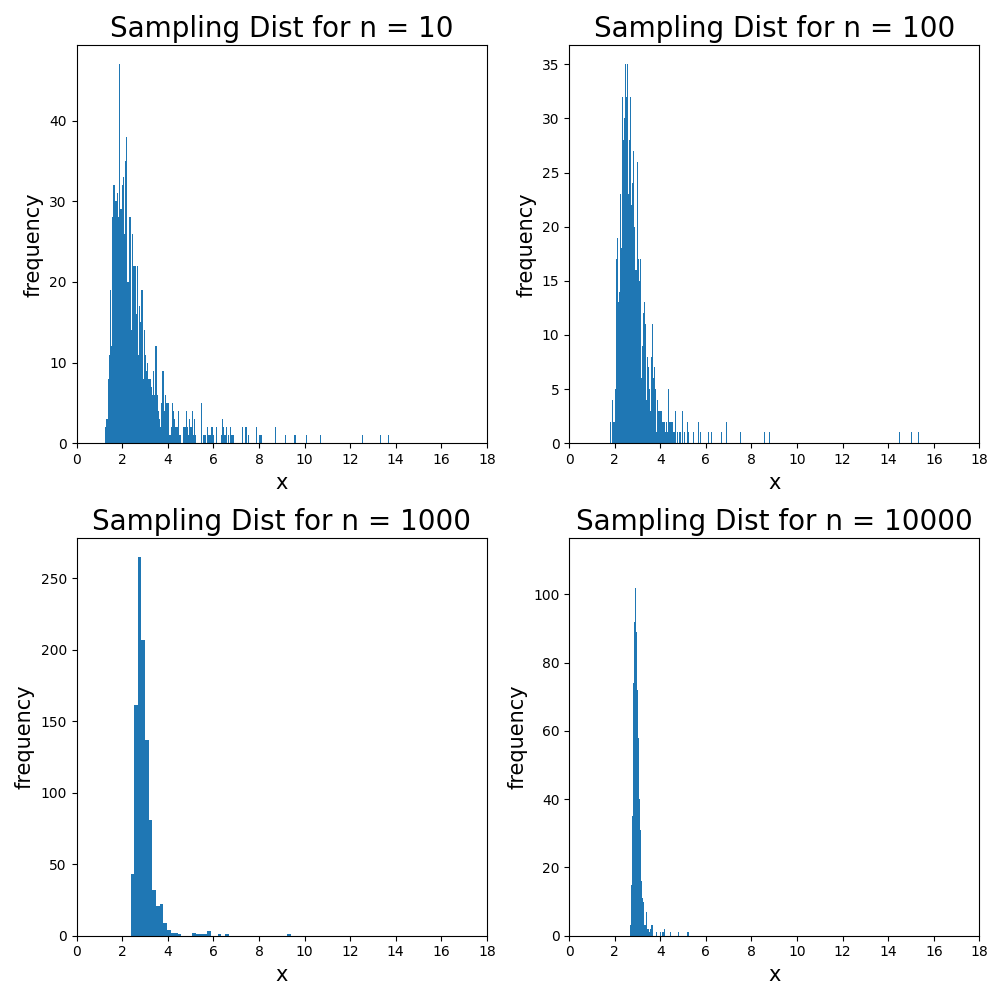
Rare-Event Estimation via Monte Carlo and Importance Sampling
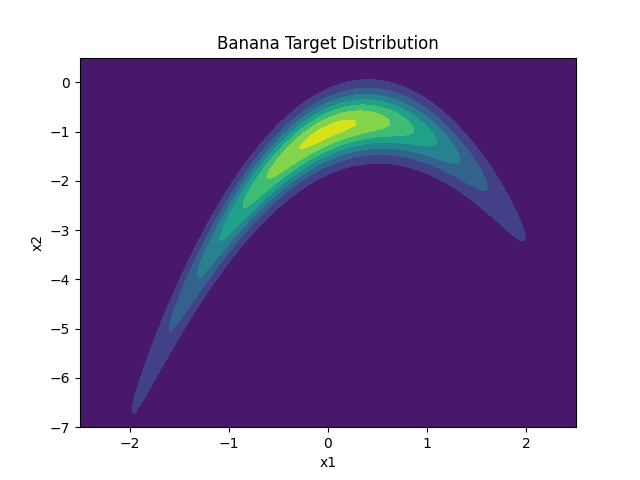
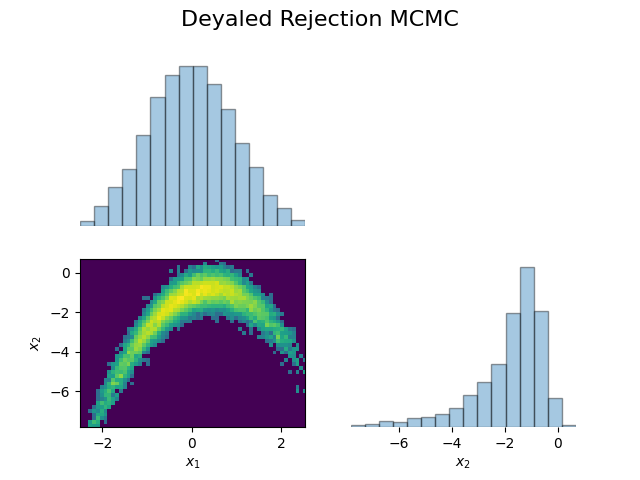
This project tackles rare-event probability estimation in stochastic systems. We first employed a naïve Monte Carlo approach on 1D and 3D random walks, then introduced an importance sampling strategy with optimized biasing distributions. Both estimators were compared under equal sample budgets using Chebyshev and CLT bounds, revealing dramatic variance reduction.
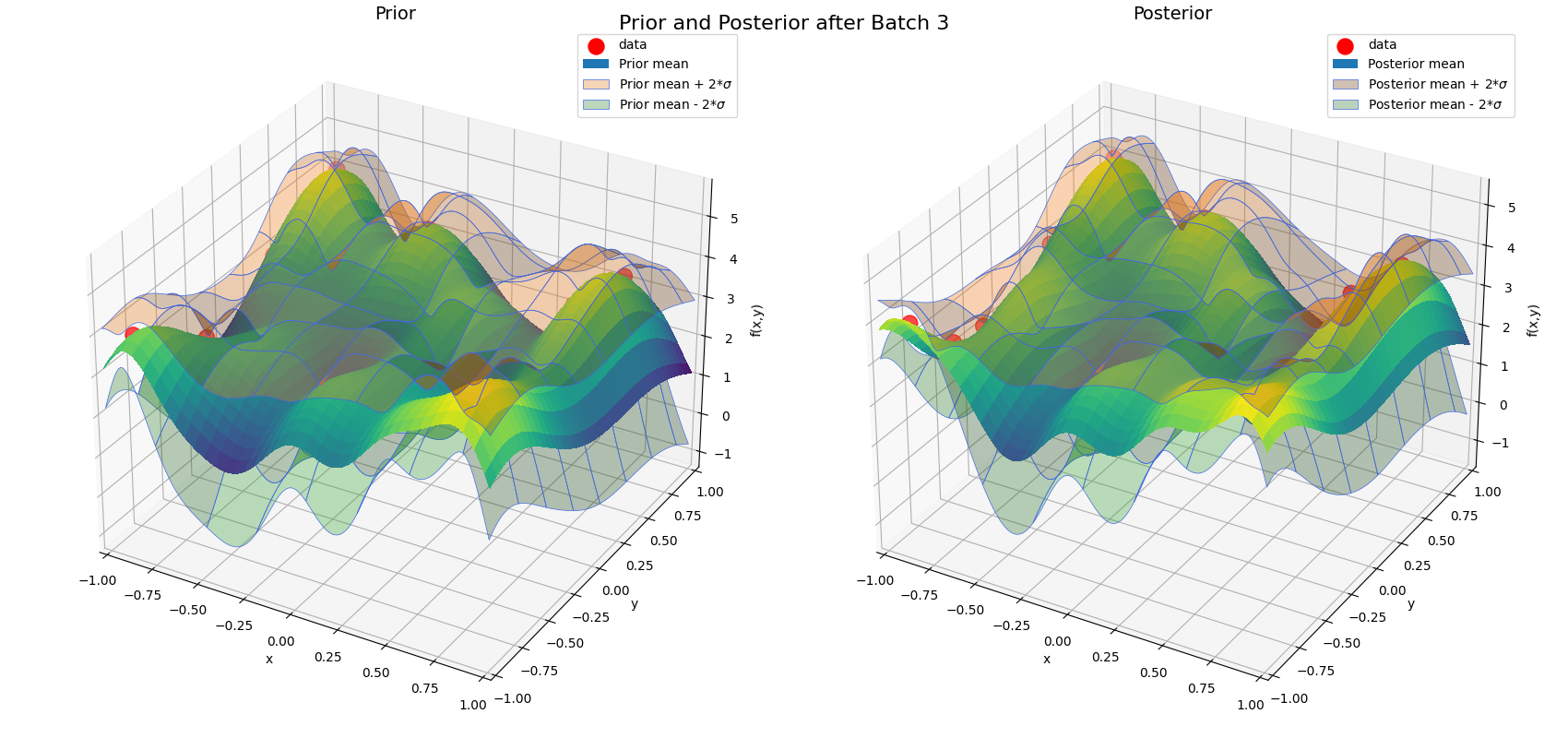
Active Object Localization using Bayesian Optimization
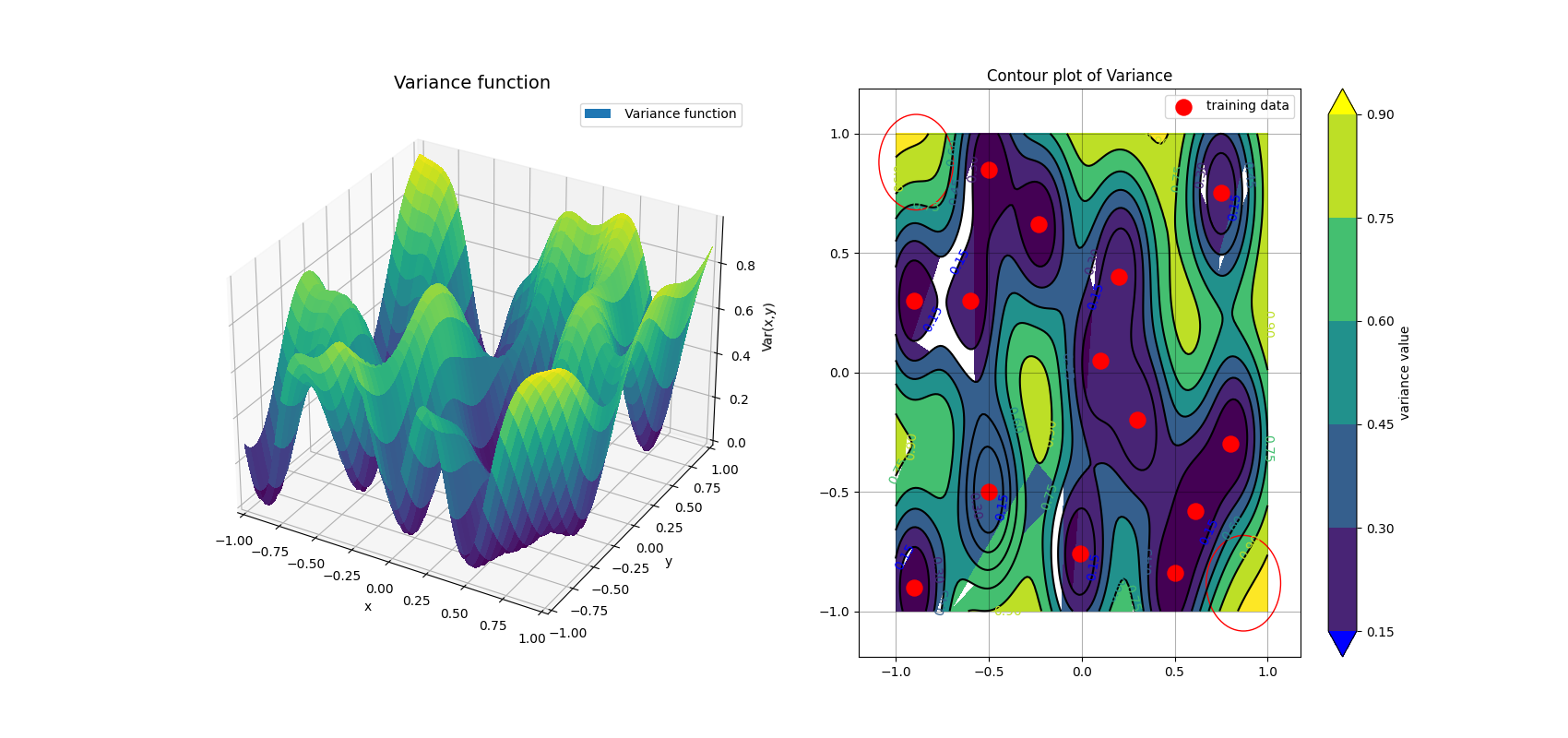
In this exploration-focused project, a robot models its environment with Gaussian Process regression and selects informative measurements via Bayesian Optimization. Expected Improvement and Probability of Improvement guide the search for a hidden target, demonstrating how uncertainty-aware policies accelerate localization.
Posterior Inference in Nonlinear Epidemiological Dynamics using MCMC
We applied Metropolis-Hastings and DRAM algorithms to infer parameters of a nonlinear SIR model from noisy data. The study investigated identifiability, noise sensitivity and predictive uncertainty, highlighting the power of Bayesian MCMC for dynamical systems.
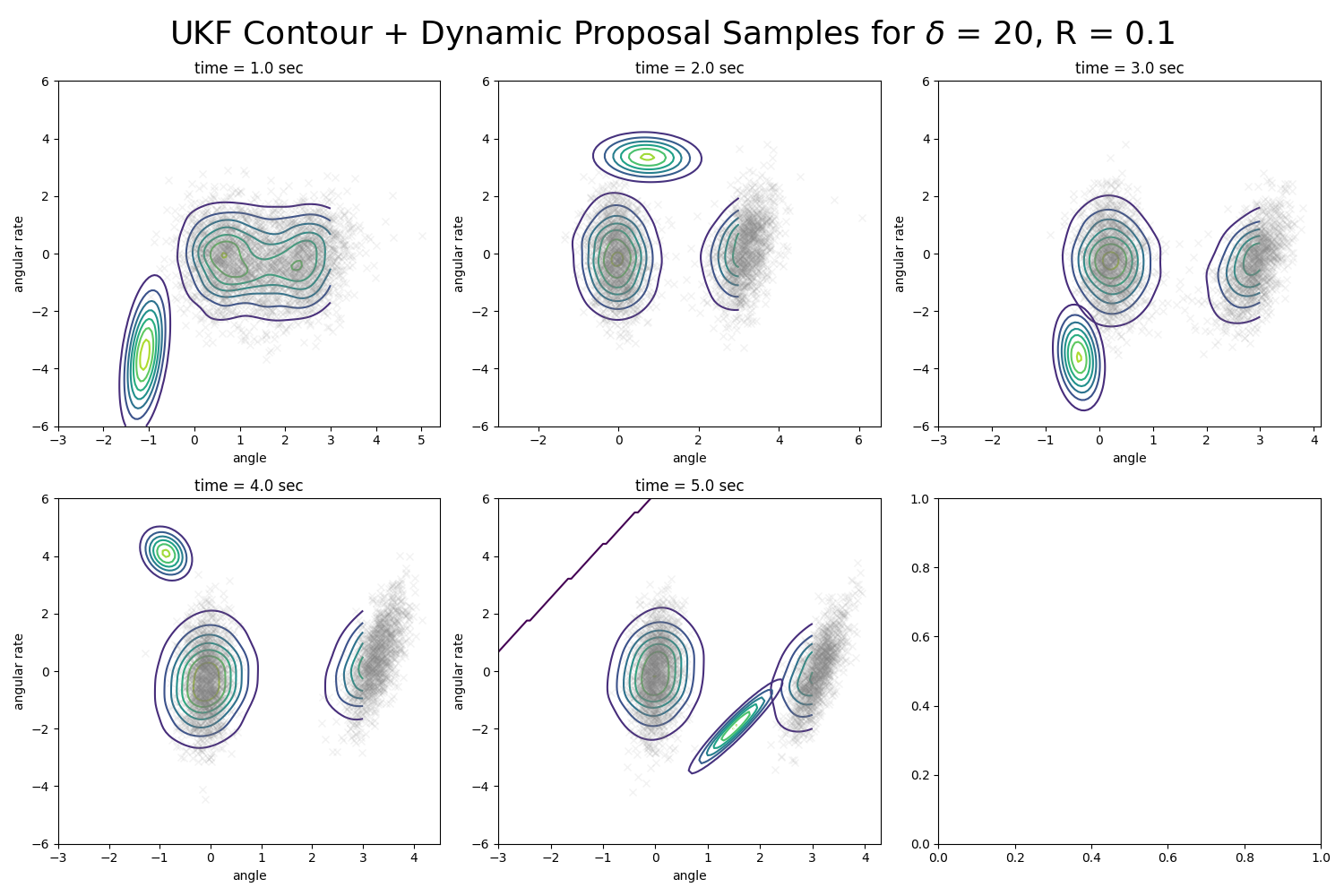
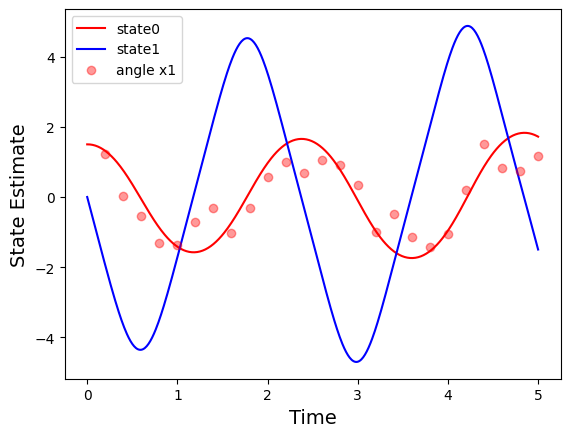
Nonlinear Filtering of Pendulum Dynamics using Gaussian and Non-Gaussian Methods
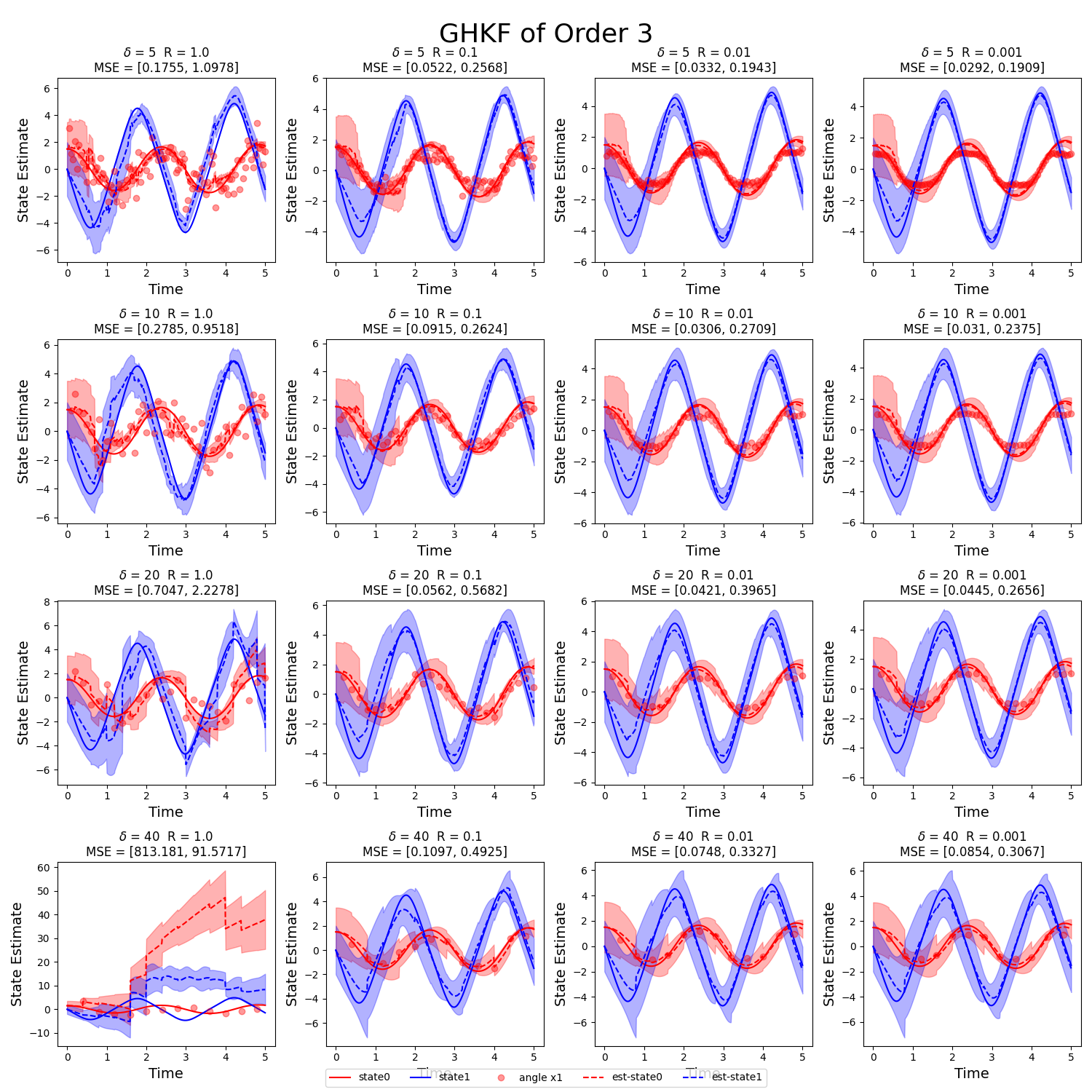
This benchmark compares Extended and Unscented Kalman filters, Gauss-Hermite filters, and Particle Filters on a nonlinear pendulum. Estimation accuracy, computational cost and robustness to non-Gaussian noise were evaluated across varying sensor noise and update rates.
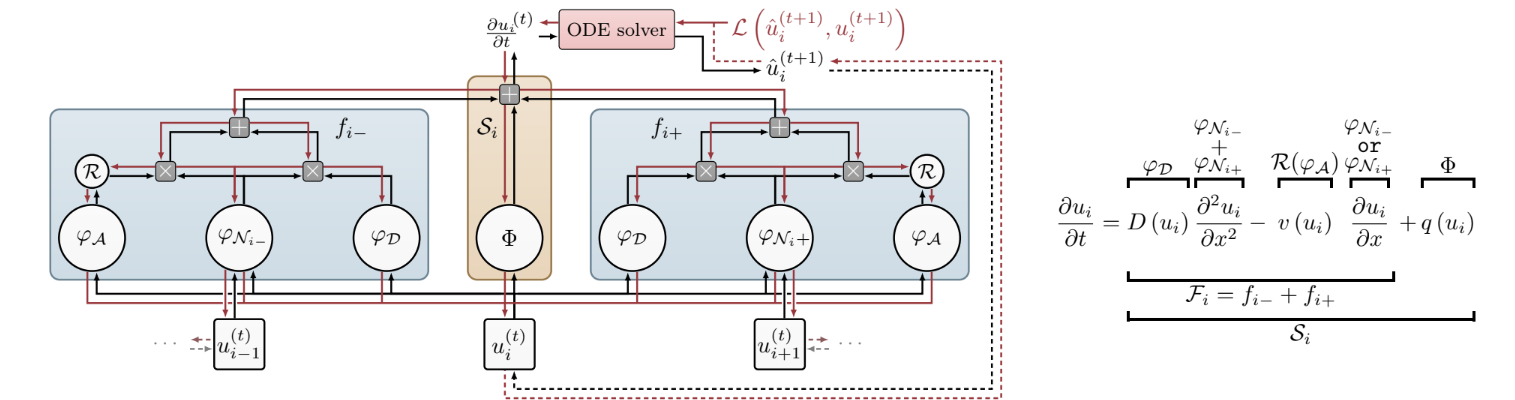
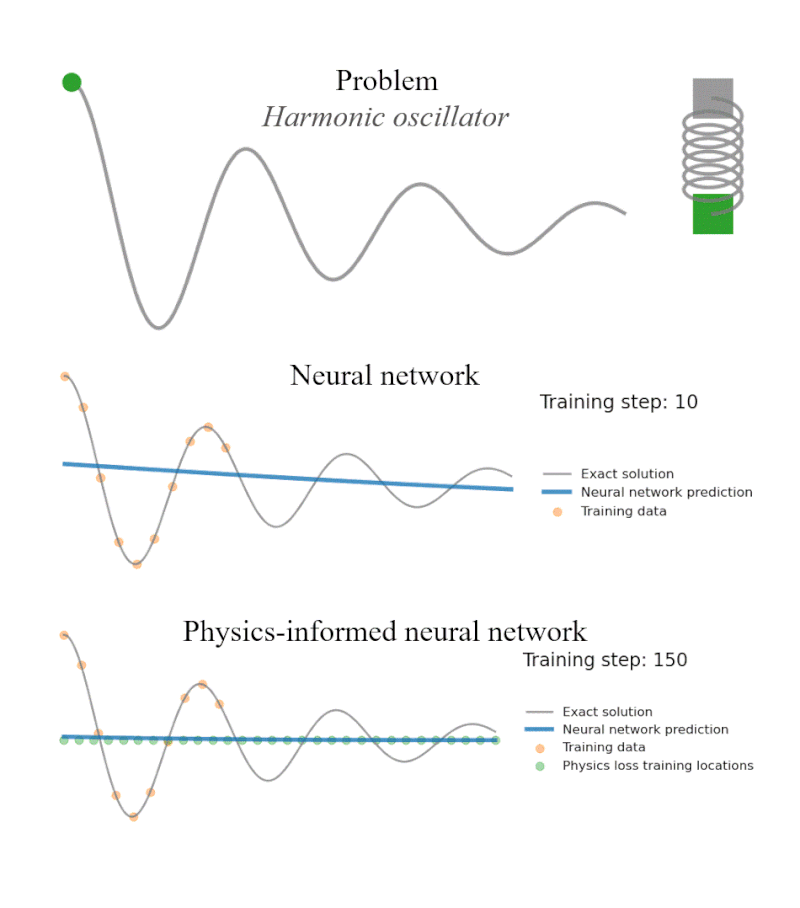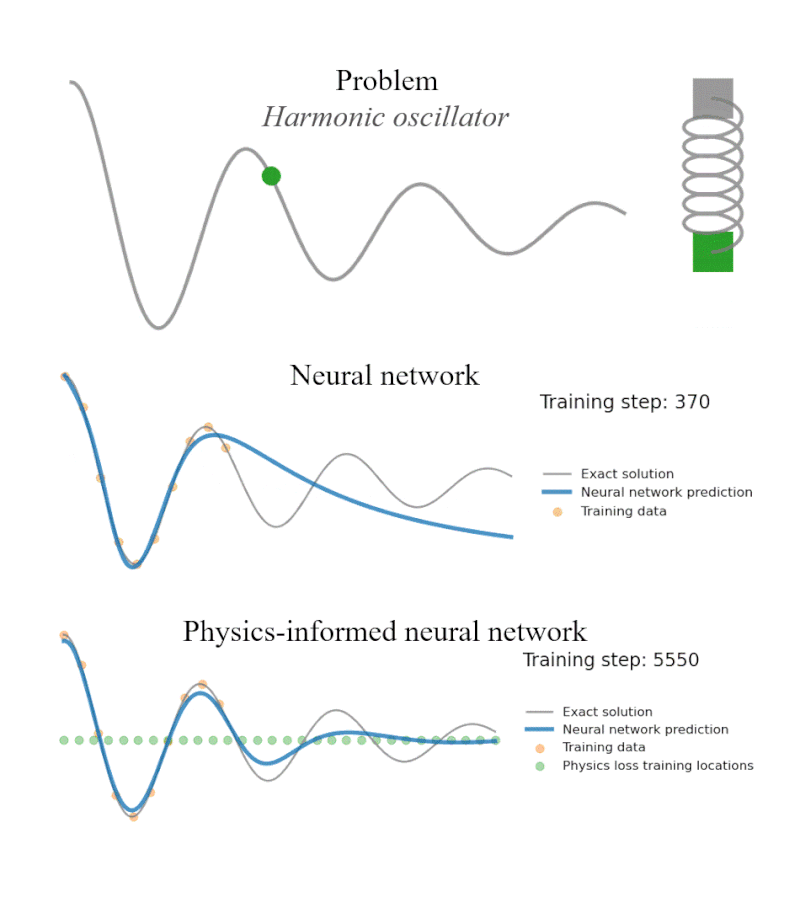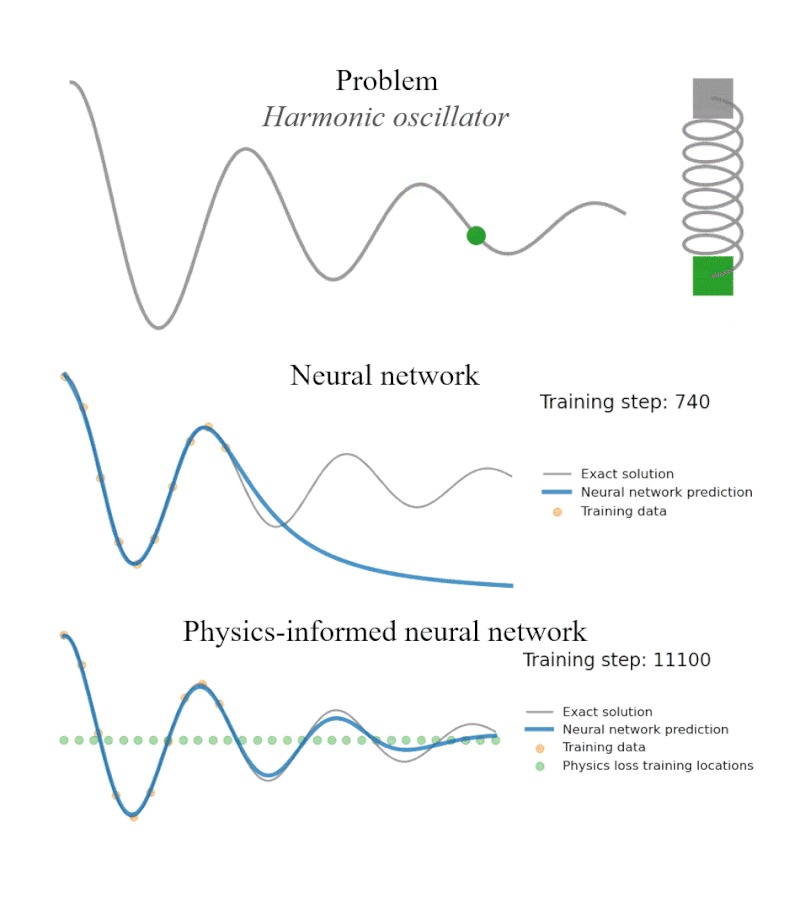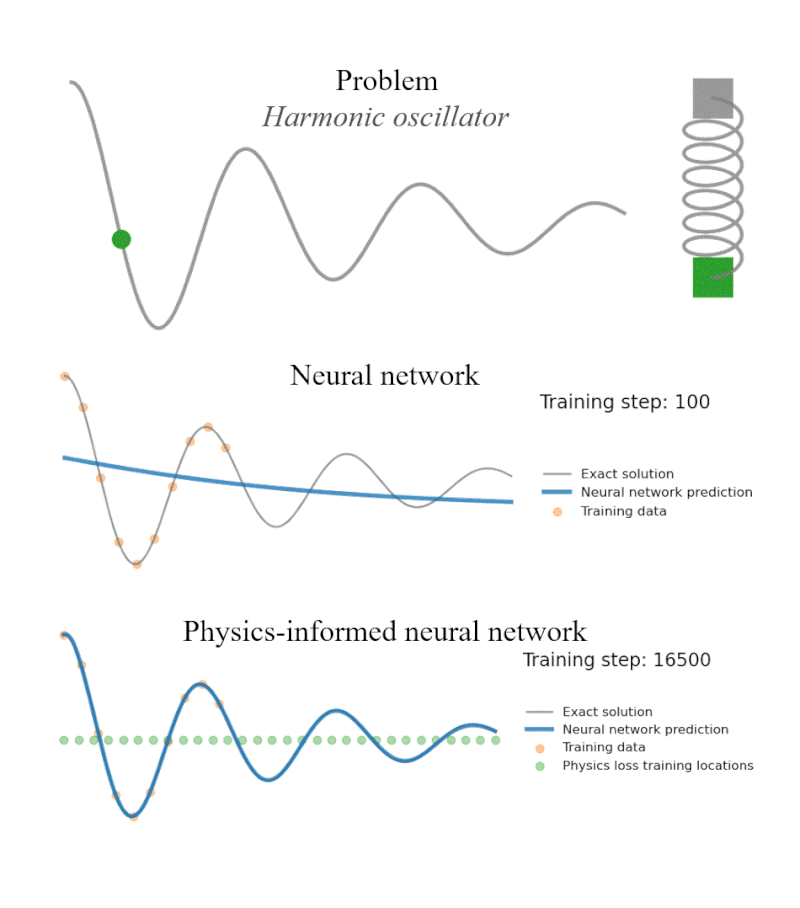
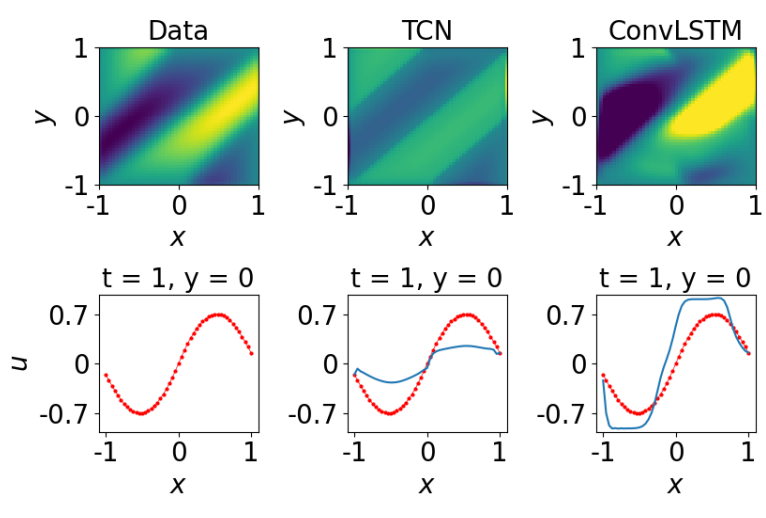
Reproducibility Study of Physics-Aware Neural Networks for PDEs
We replicated the FINN architecture to solve spatiotemporal partial differential equations, confirming its strong generalization and robustness. Experiments on Burgers', Allen–Cahn and diffusion-sorption systems showed FINN outperforming ConvLSTM, TCN and other baselines even with noisy data and longer prediction horizons.